W'Blog

Wbuildings的自勉小屋

0%

NKCTF2023

发表于 分类于 Valine：
本文字数： 74k 阅读时长 ≈ 1:07

NKCTF2024还有两周就快开始了，复现一下NKCTF2023

baby_RSA

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from Crypto.Util.number import *
nbit = 512
flag='****************************'

p=getPrime(nbit)
q=getPrime(nbit)
e=65537
n=p*q
m= bytes_to_long(bytes(flag.encode()))
P = pow(m,p,n)
Q = pow(m,q,n)
N=P*Q
phi_N=(P-1)*(Q-1)
d=inverse(e,phi_N)
dP=d%(P-1)
print('n = ',n)
print('N = ',N)
print('dP = ',dP)


n =  114101396033690088275999670914803472451228154227614098210572767821433470213124900655723605426526569384342101959232900145334500170690603208327913698128445002527020347955300595384752458477749198178791196660625870659540794807018881780680683388008090434114437818447523471527878292741702348454486217652394664664641
N =  1159977299277711167607914893426674454199208605107323826176606074354449015203832606569051328721360397610665453513201486235549374869954501563523028914285006850687275382822302821825953121223999268058107278346499657597050468069712686559045712946025472616754027552629008516489090871415609098178522863027127254404804829735621706042266140637592206366042515190385496909533329383212542170504864473944657824502882014292528444918055958758310544435120502872883857209880723535754528096143707324179005292445100655695427777453144657819474805882956064292780031599790769618615908501966912635232746588639924772530057835864082951499028
dP =  33967356791272818610254738927769774016289590226681637441101504040121743937150259930712897925893431093938385216227201268238374281750681609796883676743311872905933219290266120756315613501614208779063819499785817502677885240656957036398336462000771885589364702443157120609506628895933862241269347200444629283263

题解：

先是老生常见的dp泄露 ,然后：

$P = m^p \bmod n=m+k_1p$

$Q = m^q \bmod n=m+k_2q$

$P*Q=m^2+m(k_1p+k_2q)+k_1k_2pq$

所以copper里的多项式就出来了：$P*Q=m^2+m(P-m+Q-m) \bmod n$

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import libnum

n =  114101396033690088275999670914803472451228154227614098210572767821433470213124900655723605426526569384342101959232900145334500170690603208327913698128445002527020347955300595384752458477749198178791196660625870659540794807018881780680683388008090434114437818447523471527878292741702348454486217652394664664641
N =  1159977299277711167607914893426674454199208605107323826176606074354449015203832606569051328721360397610665453513201486235549374869954501563523028914285006850687275382822302821825953121223999268058107278346499657597050468069712686559045712946025472616754027552629008516489090871415609098178522863027127254404804829735621706042266140637592206366042515190385496909533329383212542170504864473944657824502882014292528444918055958758310544435120502872883857209880723535754528096143707324179005292445100655695427777453144657819474805882956064292780031599790769618615908501966912635232746588639924772530057835864082951499028
dP =  33967356791272818610254738927769774016289590226681637441101504040121743937150259930712897925893431093938385216227201268238374281750681609796883676743311872905933219290266120756315613501614208779063819499785817502677885240656957036398336462000771885589364702443157120609506628895933862241269347200444629283263
e = 65537

for i in range(1,e):
    P=(dP*e-1)//i+1
    if N%P==0:
        Q=N//P
        break

PR.<x> = PolynomialRing(Zmod(n))
f = P*Q - x^2 -x*(P-x+Q-x)
f = f.small_roots()
print(libnum.n2s(int(f[0])))

# NKCTF{Th1S_a_babyRSA_y0u_are_tql!!!}

解2：

一般是消项凑公因子的思路

$P^{pq} = (m^{pq})^p \bmod n=m \bmod p=m+k_1p$

$Q^{pp} = (m^{pq})^p \bmod n=m \bmod p$ ==> $Q= m \bmod p=m+k_2p$

$P^{pq}-Q=p(k_1-k_2)$

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import libnum

n =  114101396033690088275999670914803472451228154227614098210572767821433470213124900655723605426526569384342101959232900145334500170690603208327913698128445002527020347955300595384752458477749198178791196660625870659540794807018881780680683388008090434114437818447523471527878292741702348454486217652394664664641
N =  1159977299277711167607914893426674454199208605107323826176606074354449015203832606569051328721360397610665453513201486235549374869954501563523028914285006850687275382822302821825953121223999268058107278346499657597050468069712686559045712946025472616754027552629008516489090871415609098178522863027127254404804829735621706042266140637592206366042515190385496909533329383212542170504864473944657824502882014292528444918055958758310544435120502872883857209880723535754528096143707324179005292445100655695427777453144657819474805882956064292780031599790769618615908501966912635232746588639924772530057835864082951499028
dP =  33967356791272818610254738927769774016289590226681637441101504040121743937150259930712897925893431093938385216227201268238374281750681609796883676743311872905933219290266120756315613501614208779063819499785817502677885240656957036398336462000771885589364702443157120609506628895933862241269347200444629283263
e = 65537

for i in range(1,e):
    P=(dP*e-1)//i+1
    if N%P==0:
        Q=N//P
        break

p = libnum.gcd(pow(P,n,n) -Q,n)   # pow()
q = n//p
phi = (p-1)*(q-1)
d = libnum.invmod(p,phi)
m = pow(P,d,n)
print(libnum.n2s(int(m)))

# NKCTF{Th1S_a_babyRSA_y0u_are_tql!!!}

ez_math

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from Crypto.Util.number import getPrime, bytes_to_long
from secret import BITS, hints, flag

p = getPrime(BITS)
q = getPrime(BITS)
n = p * q
print(f'n = {n}')

e = 0x10001
c = pow(bytes_to_long(flag), e, n)
print(f'c = {c}')

print('Give you some boring pows:')
for i in range(len(hints)):
    print(hints[i])

"""
n = 369520637995317866367336688225182965061898803879373674073832046072914710171302486913303917853881549637806426191970292829598855375370563396182543413674021955181862907847280705741114636854238746612618069619482248639049407507041667720977392421249242597197448360531895206645794505182208390084734779667749657408715621
c = 324131338592233305486487416176106472248153652884280898177125443926549710357763331715045582842045967830200123100144721322509500306940560917086108978796500145618443920020112366546853892387011738997522207752873944151628204886591075864677988865335625452099668804529484866900390927644093597772065285222172136374562043
Give you some boring pows:
pow(6, 42762902032363446334121451790132830028099011269558028556333775251728898854654431095595000922138958455510196735338223430882428451914478079186797153527810555787441234842366353864053114538165236037883914332840687123514412294276743506313011532002136735343280737244020115917460801848337792582496228600926958548903290, n) = 4
pow(6, 141997416965295486849546892322458652502850390670128808480582247784728456230996812361056958004801816363393016360646922983916999235770803618904474553309200419301820603229504955218189709387942156848904968053547462302189568831762401075340100029630332409419313772378068180267756675141584884876543484516408660699471038, n) = 9
pow(6, 163378867981477210016607618217525067516899896304907822758749135410592905658324027908854458465871295591148114728316034699358213461728042658497873130073105697195541220650688132150216266657024774867846925219967805863946774978900772828496605795631400777090954141000078238226487076065753781167791598816872139973922682, n) = 3
pow(5, 101651508435846472131121026992982127175369332865677196032272241712711171024515826370577416844824734811581351106736224929238579734879671732717639124571916168742336862493284572465162318403582113621582374924091725060981390318743531229548188092491836655143124663368239422819562367919547196053790207486164506763679128, n) = 4
pow(8, 7202269322818255506843028035725052687541091567764933235328308385449791332345247877549905289072216053144576876979686287212194040101112899704499548530779540409356827298148385589812450437990490353926475147376495772639210184768544932563432306664067058309318707174880146258394471096033723193568453520897758319446472, n) = 3
pow(6, 64144353048545169501182177685199245042148516904337042834500662877593348281981646643392501383208437683265295103007335146323642677871717118780195730291715833681161852263549530796079671807247854056825871499261030685271618441415115259469517298003205103014921105866030173876191202772506688873744342901390437823354935, n) = 8
pow(6, 21381451016181723167060725895066415014049505634779014278166887625864449427327215547797500461069479227755098367669111715441214225957239039593398576763905277893720617421183176932026557269082618018941957166420343561757206147138371753156505766001068367671640368622010057958730400924168896291248114300463479274451645, n) = 2
pow(4, 21606807968454766520529084107175158062623274703294799705984925156349373997035743632649715867216648159433730630939058861636582120303338699113498645592338621228070481894445156769437351313971471061779425442129487317917630554305634797690296919992201174927956121524640438775183413288101169580705360562693274958339416, n) = 9
pow(2, 21606807968454766520529084107175158062623274703294799705984925156349373997035743632649715867216648159433730630939058861636582120303338699113498645592338621228070481894445156769437351313971471061779425442129487317917630554305634797690296919992201174927956121524640438775183413288101169580705360562693274958339417, n) = 6
pow(4, 10803403984227383260264542053587579031311637351647399852992462578174686998517871816324857933608324079716865315469529430818291060151669349556749322796169310614035240947222578384718675656985735530889712721064743658958815277152817398845148459996100587463978060762320219387591706644050584790352680281346637479169708, n) = 3
pow(9, 3293982057350410278459882519024200329089724149803879577174733206141551016681048848343176690789446255513117465644006032807116613436995145441651711865811812905401261777042165657533800465011922458688696664211216129846590488003282750224539553623014598025837108471148806368738631086225250952573439068109703953523338, n) = 4
pow(2, 43213615936909533041058168214350316125246549406589599411969850312698747994071487265299431734433296318867461261878117723273164240606677398226997291184677242456140963788890313538874702627942942123558850884258974635835261108611269595380593839984402349855912243049280877550366826576202339161410721125386549916678832, n) = 9
pow(7, 156359509651684605051402965560382969488421316701585527115005130492947292379802933549188085059602557600903593831240316597311439285149968787780538126741092612405335349622445040578126369183536683733294143156965518222696624206221060030916594302284630706642066420353822195108928341123726471513256217857861184609387726, n) = 9
pow(7, 170559914324671769117535654836487226009685359320636182075960576764702323732727088502920021993271666209903403463612731506055433486417625242935904916789051793747298593847158174830184596554822038310041512771676833824200302666130102306284852931958549925702330464987955245647072909056824574486147965487598401928881026, n) = 3
pow(8, 123173545998439288789112229408394321687299601293124558024610682024304903390434162304434639284627183212602142063990097609866285125123521132060847804558007316726174558714580872721495215950738261924525921590925432950469320750692763054435407707754979429841729673081392197456811651326615118306026475411557079498916218, n) = 4
pow(2, 21606807968454766520529084107175158062623274703294799705984925156349373997035743632649715867216648159433730630939058861636582120303338699113498645592338621228070481894445156769437351313971471061779425442129487317917630554305634797690296919992201174927956121524640438775183413288101169580705360562693274958339416, n) = 3
pow(3, 6587964114700820556919765038048400658179448299607759154349466412283102033362097696686353381578892511026234931288012065614233226873990290883303423731623625810802523554084331315067600930023844917377393328422432259693180976006565500449079107246029196051674216942297612737477262172450501905146878136219407907046676, n) = 4
pow(7, 146900004342901005519726059203387905743111231159623333298786259340649199259667124880775175860427705602975071010583553281005991812801779033020769274211420710213704563866848310994325033574484679477677016014418321661821714582236428708141287327064859146436371562752616380650770729341741997594308364878898526065859626, n) = 4
pow(5, 172192380036714150788905270808196199818277334366508682218739812159577144024191963252552116624193235000074634457087111471641800814071769221933018962135503876997163938949365614056098717522475180216291316295788774044033481065993544994610614082708563841846852650913646728169671510827052772868386414581035580266356334, n) = 3
pow(8, 68789042322037899901399142739922213531190892214327212247633649397602243027562329029767224931385807659445647908974735092145336602662873465734923450809783198772444106655438821950560058413359621316189435942839212247873870560114926459781136160541556773230183543715576244986800296759341282346581691226676298068904581, n) = 6
pow(5, 159624441075769368394142197503800917105605266793330527400563601282696932962732683048452274321445695181246055818189076528484173940458256745774766217433996778905066039826859919029954611118842967545793750205189398662362981005947945407568116603784658538931110792205205160154125544664182868277733116044735541284338342, n) = 9
pow(8, 14404538645636511013686056071450105375082183135529866470656616770899582664690495755099810578144432106289153753959372574424388080202225799408999097061559080818713654596296771179624900875980980707852950294752991545278420369537089865126864613328134116618637414349760292516788942192067446387136907041795516638892944, n) = 9
"""

题解：

$a^{e_1} = 3 \bmod n$

$a^{e_2} = 9 \bmod n$

所以 $a^{2e_1}\equiv a^{e_2} \bmod n$ ==> $a^{2e_1-e_2}=1 \bmod n$

由欧拉定理得，$2e_1-e_2=\varphi(n)$

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import libnum

n = 369520637995317866367336688225182965061898803879373674073832046072914710171302486913303917853881549637806426191970292829598855375370563396182543413674021955181862907847280705741114636854238746612618069619482248639049407507041667720977392421249242597197448360531895206645794505182208390084734779667749657408715621
c = 324131338592233305486487416176106472248153652884280898177125443926549710357763331715045582842045967830200123100144721322509500306940560917086108978796500145618443920020112366546853892387011738997522207752873944151628204886591075864677988865335625452099668804529484866900390927644093597772065285222172136374562043
e = 0x10001

a73 = 170559914324671769117535654836487226009685359320636182075960576764702323732727088502920021993271666209903403463612731506055433486417625242935904916789051793747298593847158174830184596554822038310041512771676833824200302666130102306284852931958549925702330464987955245647072909056824574486147965487598401928881026
a79 = 156359509651684605051402965560382969488421316701585527115005130492947292379802933549188085059602557600903593831240316597311439285149968787780538126741092612405335349622445040578126369183536683733294143156965518222696624206221060030916594302284630706642066420353822195108928341123726471513256217857861184609387726


phi = 2*a73 - a79
d = libnum.invmod(e,phi)
m = pow(c,d,n)
print(libnum.n2s(m))
# NKCTF{d15cr373_L0g_15_R3DuC710n_f0R_f4C70r1nG}

ezRSA

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from Crypto.Util.number import *
from secret import flag

m1 = bytes_to_long(flag[:len(flag)//3])
m2 = bytes_to_long(flag[len(flag)//3:])

def gen():
    prime_list  = []
    for i in range(4):
        prime_list.append(getPrime(512))
    return sorted(prime_list)

prime_list = gen()
p,q,r,t = prime_list[0],prime_list[3],prime_list[1],prime_list[2]
e = 65537
n = p*q*r*t
phi = (p-1)*(q-1)*(r-1)*(t-1)
c1 = pow(m1,e,p*q)
p1 = getPrime(512)
q1 = getPrime(512)
N = p1*q1
c2 = pow(m2,p1,N)
c3 = pow(m2,q1,N)
print(f'n = {n}')
print(f'phi = {phi}')
print(f'c1 = {c1}')
print(f'N = {N}')
print(f'c2 = {c2}')
print(f'c3 = {c3}')

'''
n = 8836130216343708623415307573630337110573363595188748983290313549413242332143945452914800845282478216810685733227137911630239808895196748125078747600505626165666334675100147790578546682128517668100858766784733351894480181877144793496927464058323582165412552970999921215333509253052644024478417393146000490808639363681195799826541558906527985336104761974023394438549055804234997654701266967731137282297623426318212701157416397999108259257077847307874122736921265599854976855949680133804464839768470200425669609996841568545945133611190979810786943246285103031363790663362165522662820344917056587244701635831061853354597
phi = 8836130216343708623415307573630337110573363595188748983290313549413242332143945452914800845282478216810685733227137911630239808895196748125078747600505622503351461565956106005118029537938273153581675065762015952483687057805462728186901563990429998916382820576211887477098611684072561849314986341226981300596338314989867731725668312057134075244816223120038573374383949718714549930261073576391501671722900294331289082826058292599838631513746370889828026039555245672195833927609280773258978856664434349221972568651378808050580665443131001632395175205804045958846124475183825589672204752895252723130454951830966138888560
c1 = 78327207863361017953496121356221173288422862370301396867341957979087627011991738176024643637029313969241151622985226595093079857523487726626882109114134910056673489916408854152274726721451884257677533593174371742411008169082367666168983943358876017521749198218529804830864940274185360506199116451280975188409
N = 157202814866563156513184271957553223260772141845129283711146204376449001653397810781717934720804041916333174673656579086498762693983380365527400604554663873045166444369504886603233275868192688995284322277504050322927511160583280269073338415758019142878016084536129741435221345599028001581385308324407324725353
c2 = 63355788175487221030596314921407476078592001060627033831694843409637965350474955727383434406640075122932939559532216639739294413008164038257338675094324172634789610307227365830016457714456293397466445820352804725466971828172010276387616894829328491068298742711984800900411277550023220538443014162710037992032
c3 = 9266334096866207047544089419994475379619964393206968260875878305040712629590906330073542575719856965053269812924808810766674072615270535207284077081944428011398767330973702305174973148018082513467080087706443512285098600431136743009829009567065760786940706627087366702015319792328141978938111501345426931078
'''

题解：

第一部分观察细节：知道n和phi，直接可以搜到相关分解n的脚本（已知n和phi，分解n）

第二部分同baby_RSA：

$c_2^{q_1p_1}=m_2 \bmod p_1 $

$c_3=m_2 \bmod p_1$

$c_2^N-c_3=p_1(k_1-k_2)$ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import gmpy2
import libnum
from math import isqrt
from random import randrange
from gmpy2 import is_prime
from libnum import gcd

n = 8836130216343708623415307573630337110573363595188748983290313549413242332143945452914800845282478216810685733227137911630239808895196748125078747600505626165666334675100147790578546682128517668100858766784733351894480181877144793496927464058323582165412552970999921215333509253052644024478417393146000490808639363681195799826541558906527985336104761974023394438549055804234997654701266967731137282297623426318212701157416397999108259257077847307874122736921265599854976855949680133804464839768470200425669609996841568545945133611190979810786943246285103031363790663362165522662820344917056587244701635831061853354597
phi = 8836130216343708623415307573630337110573363595188748983290313549413242332143945452914800845282478216810685733227137911630239808895196748125078747600505622503351461565956106005118029537938273153581675065762015952483687057805462728186901563990429998916382820576211887477098611684072561849314986341226981300596338314989867731725668312057134075244816223120038573374383949718714549930261073576391501671722900294331289082826058292599838631513746370889828026039555245672195833927609280773258978856664434349221972568651378808050580665443131001632395175205804045958846124475183825589672204752895252723130454951830966138888560
c1 = 78327207863361017953496121356221173288422862370301396867341957979087627011991738176024643637029313969241151622985226595093079857523487726626882109114134910056673489916408854152274726721451884257677533593174371742411008169082367666168983943358876017521749198218529804830864940274185360506199116451280975188409
N = 157202814866563156513184271957553223260772141845129283711146204376449001653397810781717934720804041916333174673656579086498762693983380365527400604554663873045166444369504886603233275868192688995284322277504050322927511160583280269073338415758019142878016084536129741435221345599028001581385308324407324725353
c2 = 63355788175487221030596314921407476078592001060627033831694843409637965350474955727383434406640075122932939559532216639739294413008164038257338675094324172634789610307227365830016457714456293397466445820352804725466971828172010276387616894829328491068298742711984800900411277550023220538443014162710037992032
c3 = 9266334096866207047544089419994475379619964393206968260875878305040712629590906330073542575719856965053269812924808810766674072615270535207284077081944428011398767330973702305174973148018082513467080087706443512285098600431136743009829009567065760786940706627087366702015319792328141978938111501345426931078
e = 65537

def factorize(N, phi):    # 只能分解两个因子
    """
    Recovers the prime factors from a modulus if Euler's totient is known.
    This method only works for a modulus consisting of 2 primes!
    :param N: the modulus
    :param phi: Euler's totient, the order of the multiplicative group modulo N
    :return: a tuple containing the prime factors, or None if the factors were not found
    """
    s = N + 1 - phi
    d = s ** 2 - 4 * N
    p = int(s - isqrt(d)) // 2
    q = int(s + isqrt(d)) // 2
    return p, q if p * q == N else None


def factorize_multi_prime(N, phi):   # 能分解出多个因子
    """
    Recovers the prime factors from a modulus if Euler's totient is known.
    This method works for a modulus consisting of any number of primes, but is considerably be slower than factorize.
    More information: Hinek M. J., Low M. K., Teske E., "On Some Attacks on Multi-prime RSA" (Section 3)
    :param N: the modulus
    :param phi: Euler's totient, the order of the multiplicative group modulo N
    :return: a tuple containing the prime factors
    """
    prime_factors = set()
    factors = [N]
    while len(factors) > 0:
        # Element to factorize.
        N = factors[0]

        w = randrange(2, N - 1)
        i = 1
        while phi % (2 ** i) == 0:
            sqrt_1 = pow(w, phi // (2 ** i), N)
            if sqrt_1 > 1 and sqrt_1 != N - 1:
                # We can remove the element to factorize now, because we have a factorization.
                factors = factors[1:]

                p = gcd(N, sqrt_1 + 1)
                q = N // p

                if is_prime(p):
                    prime_factors.add(p)
                elif p > 1:
                    factors.append(p)

                if is_prime(q):
                    prime_factors.add(q)
                elif q > 1:
                    factors.append(q)

                # Continue in the outer loop
                break

            i += 1

    return tuple(prime_factors)

a = factorize_multi_prime(n,phi)
prime_list = sorted(a)
p,q,r,t = prime_list[0],prime_list[3],prime_list[1],prime_list[2]

d = libnum.invmod(e,(p-1)*(q-1))
m1 = pow(c1,d,p*q)
m1 = libnum.n2s(m1)

p1 = libnum.gcd(pow(c2,N,N) -c3,N)   # pow()
q1 = N//p1

s,s1,s2 = gmpy2.gcdext(p1,q1)
m2  =pow(c2,s1,N)*pow(c3,s2,N)%N
m2 = libnum.n2s(int(m2))
print(m1+m2)
# NKCTF{it_i5_e45y_th4t_Kn0wn_phi_4nd_N_dec0mp0ses_N_w1th_th3_s4m3_c0mm0n_n_but_pq}

real_MT

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import random
import signal

def guess_number_1():
    randoms = []
    for _ in range(208):
        randoms.append(random.getrandbits(96))

    print("randoms = "+str(randoms))
    number = str(random.getrandbits(96))
    guess = str(input("Guess after number:"))
    if guess != number:
        print("Wrong Number! Guess again.")
        exit(0)

def guess_number_2():
    number = str(random.getrandbits(96))
    randoms = []
    for _ in range(627):
        randoms.append(random.getrandbits(32))

    print("randoms = "+str(randoms))
    guess = str(input("Guess pre number:"))
    if guess != number:
        print("Wrong Number! Guess again.")
        exit(0)

def guess_number_3():

    def _int32(x):
        return int(0xFFFFFFFF & x)  
    def init(seed):
        mt = [0] * 624
        mt[0] = seed
        for i in range(1, 624):
            mt[i] = _int32(1812433253 * (mt[i - 1] ^ mt[i - 1] >> 30) + i)
        return mt[-1]
    number = random.getrandbits(32)
    print("last number = "+ str(init(number)))
    guess = int(str(input("Guess seed number:")))
    if guess != number:
        print("Wrong Number! Guess again.")
        exit(0)

def guess_number_4():
    def extract_number(y):
        y = y ^ y >> 11
        y = y ^ y << 7 & 2636928640
        y = y ^ y << 15 & 4022730752
        y = y ^ y >> 18
        return y&0xffffffff

    number = random.getrandbits(32)
    print("extract number = "+ str(extract_number(number)))
    guess = int(str(input("Guess be extracted number:")))
    if guess != number:
        print("Wrong Number! Guess again.")
        exit(0)
    

print("Welcome to the Mersenne Twister basic challenge. Please try to solve 20 challenges in 60 seconds.")
signal.alarm(60)

for i in range(20):
    print("Round: "+str(i+1))
    random.choice([guess_number_1,guess_number_2,guess_number_3,guess_number_4])()
    print("Good job!")

flag = open('/flag').read()
print("Congratulations on passing the challenge. This is your flag: " + str(flag))

题解:

移步MT19937 实战 | W’Blog (wbuildings.github.io)

fake_MT

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import random
import signal

def guess_number_1():
    randoms = []
    for _ in range(208):
        randoms.append(random.getrandbits(96))

    print("randoms = "+str(randoms))
    number = str(random.getrandbits(96))
    guess = str(input("Guess after number:"))
    if guess != number:
        print("Wrong Number! Guess again.")
        exit(0)

def guess_number_2():
    number = str(random.getrandbits(96))
    randoms = []
    for _ in range(627):
        randoms.append(random.getrandbits(32))

    print("randoms = "+str(randoms))
    guess = str(input("Guess pre number:"))
    if guess != number:
        print("Wrong Number! Guess again.")
        exit(0)

def guess_number_3():

    def _int32(x):
        return int(0xFFFFFFFF & x)  
    def init(seed):
        mt = [0] * 624
        mt[0] = seed
        for i in range(1, 624):
            mt[i] = _int32(1812433253 * (mt[i - 1] ^ mt[i - 1] >> 30) + i)
        return mt[-1]
    number = random.getrandbits(32)
    print("last number = "+ str(init(number)))
    guess = int(str(input("Guess seed number:")))
    if guess != number:
        print("Wrong Number! Guess again.")
        exit(0)

def guess_number_4():
    def extract_number(y):
        y = y ^ y >> 11
        y = y ^ y << 7 & 2636928640
        y = y ^ y << 15 & 4022730752
        y = y ^ y >> 18
        return y&0xffffffff

    number = random.getrandbits(32)
    print("extract number = "+ str(extract_number(number)))
    guess = int(str(input("Guess be extracted number:")))
    if guess != number:
        print("Wrong Number! Guess again.")
        exit(0)
    

print("Welcome to the Mersenne Twister basic challenge. Please try to solve 20 challenges in 60 seconds.")
signal.alarm(60)

for i in range(20):
    print("Round: "+str(i+1))
    random.choice([guess_number_1,guess_number_2,guess_number_3,guess_number_4])()
    print("Good job!")

flag = open('/flag').read()
print("Congratulations on passing the challenge. This is your flag: " + str(flag))


题解：

题目源码不说和real_MT长得像，简直是一模一样，一说这题是python2的环境

题解如上，和real_MT一样

同上，移步MT19937 实战 | W’Blog (wbuildings.github.io)

ez_polynomial

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#sage
from Crypto.Util.number import *
flag = list(bytearray(''))
p = getPrime(16)
R.<y> = PolynomialRing(GF(p))
while True:
    P1 = R.random_element(degree=(ZZ.random_element(len(flag), 2*len(flag))))
    Q1 = R.random_element(degree=(ZZ.random_element(len(flag), 2*len(flag))))
    if P1.is_irreducible() and Q1.is_irreducible():
        P = P1
        Q = Q1
        break
e = 65537
N = P*Q
S.<x> = R.quotient(N)
c = S(flag) ^ e
print("P:" + str(p) + "\n")
print("N:" + str(N) + "\n")
print("C:" + str(c))

#P:40031
#N:24096*y^93 + 38785*y^92 + 17489*y^91 + 9067*y^90 + 1034*y^89 + 6534*y^88 + 35818*y^87 + 22046*y^86 + 12887*y^85 + 445*y^84 + 26322*y^83 + 37045*y^82 + 4486*y^81 + 3503*y^80 + 1184*y^79 + 38471*y^78 + 8012*y^77 + 36561*y^76 + 19429*y^75 + 35227*y^74 + 10813*y^73 + 26341*y^72 + 29474*y^71 + 2059*y^70 + 16068*y^69 + 31597*y^68 + 14685*y^67 + 9266*y^66 + 31019*y^65 + 6171*y^64 + 385*y^63 + 28986*y^62 + 9912*y^61 + 10632*y^60 + 33741*y^59 + 12634*y^58 + 21179*y^57 + 35548*y^56 + 17894*y^55 + 7152*y^54 + 9440*y^53 + 4004*y^52 + 2600*y^51 + 12281*y^50 + 22*y^49 + 17314*y^48 + 32694*y^47 + 7693*y^46 + 6567*y^45 + 19897*y^44 + 27329*y^43 + 8799*y^42 + 36348*y^41 + 33963*y^40 + 23730*y^39 + 27685*y^38 + 29037*y^37 + 14622*y^36 + 29608*y^35 + 39588*y^34 + 23294*y^33 + 757*y^32 + 20140*y^31 + 19511*y^30 + 1469*y^29 + 3898*y^28 + 6630*y^27 + 19610*y^26 + 11631*y^25 + 7188*y^24 + 11683*y^23 + 35611*y^22 + 37286*y^21 + 32139*y^20 + 20296*y^19 + 36426*y^18 + 25340*y^17 + 36204*y^16 + 37787*y^15 + 31256*y^14 + 505*y^13 + 27508*y^12 + 20885*y^11 + 32037*y^10 + 31236*y^9 + 7929*y^8 + 27195*y^7 + 28980*y^6 + 11863*y^5 + 16025*y^4 + 16389*y^3 + 570*y^2 + 36547*y + 10451
#C:3552*x^92 + 6082*x^91 + 25295*x^90 + 35988*x^89 + 26052*x^88 + 16987*x^87 + 12854*x^86 + 25117*x^85 + 25800*x^84 + 30297*x^83 + 5589*x^82 + 23233*x^81 + 14449*x^80 + 4712*x^79 + 35719*x^78 + 1696*x^77 + 35653*x^76 + 13995*x^75 + 13715*x^74 + 4578*x^73 + 37366*x^72 + 25260*x^71 + 28865*x^70 + 36120*x^69 + 7047*x^68 + 10497*x^67 + 19160*x^66 + 17939*x^65 + 14850*x^64 + 6705*x^63 + 17805*x^62 + 30083*x^61 + 2400*x^60 + 10685*x^59 + 15272*x^58 + 2225*x^57 + 13194*x^56 + 14251*x^55 + 31016*x^54 + 10189*x^53 + 35040*x^52 + 7042*x^51 + 29206*x^50 + 39363*x^49 + 32608*x^48 + 38614*x^47 + 5528*x^46 + 20119*x^45 + 13439*x^44 + 25468*x^43 + 30056*x^42 + 19720*x^41 + 21808*x^40 + 3712*x^39 + 25243*x^38 + 10606*x^37 + 16247*x^36 + 36106*x^35 + 17287*x^34 + 36276*x^33 + 1407*x^32 + 28839*x^31 + 8459*x^30 + 38863*x^29 + 435*x^28 + 913*x^27 + 36619*x^26 + 15572*x^25 + 9363*x^24 + 36837*x^23 + 17925*x^22 + 38567*x^21 + 38709*x^20 + 13582*x^19 + 35038*x^18 + 31121*x^17 + 8933*x^16 + 1666*x^15 + 21940*x^14 + 25585*x^13 + 840*x^12 + 21938*x^11 + 20143*x^10 + 28507*x^9 + 5947*x^8 + 20289*x^7 + 32196*x^6 + 924*x^5 + 370*x^4 + 14849*x^3 + 10780*x^2 + 14035*x + 15327

题解：

多项式RSA ，先分解一下N，得到 phi

多项式的phi，$\varphi=p^n-1$ ，p为GF(p)的模数，n为此多项式最高项次数

所以这里的phi等于： $\varphi(N)=(p^n-1)*(p^n-1)$

然后常规解再取多项式的系数就行

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#Sage
#已知p,n,m^e

e = 65537
p = 40031
S.<x> = PolynomialRing(GF(p))
y = x
N=24096*y^93 + 38785*y^92 + 17489*y^91 + 9067*y^90 + 1034*y^89 + 6534*y^88 + 35818*y^87 + 22046*y^86 + 12887*y^85 + 445*y^84 + 26322*y^83 + 37045*y^82 + 4486*y^81 + 3503*y^80 + 1184*y^79 + 38471*y^78 + 8012*y^77 + 36561*y^76 + 19429*y^75 + 35227*y^74 + 10813*y^73 + 26341*y^72 + 29474*y^71 + 2059*y^70 + 16068*y^69 + 31597*y^68 + 14685*y^67 + 9266*y^66 + 31019*y^65 + 6171*y^64 + 385*y^63 + 28986*y^62 + 9912*y^61 + 10632*y^60 + 33741*y^59 + 12634*y^58 + 21179*y^57 + 35548*y^56 + 17894*y^55 + 7152*y^54 + 9440*y^53 + 4004*y^52 + 2600*y^51 + 12281*y^50 + 22*y^49 + 17314*y^48 + 32694*y^47 + 7693*y^46 + 6567*y^45 + 19897*y^44 + 27329*y^43 + 8799*y^42 + 36348*y^41 + 33963*y^40 + 23730*y^39 + 27685*y^38 + 29037*y^37 + 14622*y^36 + 29608*y^35 + 39588*y^34 + 23294*y^33 + 757*y^32 + 20140*y^31 + 19511*y^30 + 1469*y^29 + 3898*y^28 + 6630*y^27 + 19610*y^26 + 11631*y^25 + 7188*y^24 + 11683*y^23 + 35611*y^22 + 37286*y^21 + 32139*y^20 + 20296*y^19 + 36426*y^18 + 25340*y^17 + 36204*y^16 + 37787*y^15 + 31256*y^14 + 505*y^13 + 27508*y^12 + 20885*y^11 + 32037*y^10 + 31236*y^9 + 7929*y^8 + 27195*y^7 + 28980*y^6 + 11863*y^5 + 16025*y^4 + 16389*y^3 + 570*y^2 + 36547*y + 10451
C=3552*x^92 + 6082*x^91 + 25295*x^90 + 35988*x^89 + 26052*x^88 + 16987*x^87 + 12854*x^86 + 25117*x^85 + 25800*x^84 + 30297*x^83 + 5589*x^82 + 23233*x^81 + 14449*x^80 + 4712*x^79 + 35719*x^78 + 1696*x^77 + 35653*x^76 + 13995*x^75 + 13715*x^74 + 4578*x^73 + 37366*x^72 + 25260*x^71 + 28865*x^70 + 36120*x^69 + 7047*x^68 + 10497*x^67 + 19160*x^66 + 17939*x^65 + 14850*x^64 + 6705*x^63 + 17805*x^62 + 30083*x^61 + 2400*x^60 + 10685*x^59 + 15272*x^58 + 2225*x^57 + 13194*x^56 + 14251*x^55 + 31016*x^54 + 10189*x^53 + 35040*x^52 + 7042*x^51 + 29206*x^50 + 39363*x^49 + 32608*x^48 + 38614*x^47 + 5528*x^46 + 20119*x^45 + 13439*x^44 + 25468*x^43 + 30056*x^42 + 19720*x^41 + 21808*x^40 + 3712*x^39 + 25243*x^38 + 10606*x^37 + 16247*x^36 + 36106*x^35 + 17287*x^34 + 36276*x^33 + 1407*x^32 + 28839*x^31 + 8459*x^30 + 38863*x^29 + 435*x^28 + 913*x^27 + 36619*x^26 + 15572*x^25 + 9363*x^24 + 36837*x^23 + 17925*x^22 + 38567*x^21 + 38709*x^20 + 13582*x^19 + 35038*x^18 + 31121*x^17 + 8933*x^16 + 1666*x^15 + 21940*x^14 + 25585*x^13 + 840*x^12 + 21938*x^11 + 20143*x^10 + 28507*x^9 + 5947*x^8 + 20289*x^7 + 32196*x^6 + 924*x^5 + 370*x^4 + 14849*x^3 + 10780*x^2 + 14035*x + 15327
e = 65537

q1, q2 = N.factor()		# 分解多项式 N
q1, q2 = q1[0], q2[0]

phi = (p**q1.degree() - 1) * (p**q2.degree() - 1) 	# 求φ，注意求法
assert gcd(e, phi) == 1
d = inverse_mod(e, phi)
m = pow(C,d,N)

flag = bytes(m.coefficients())		# 取多项式系数
print("Flag: ", flag.decode())

# NKCTF{We_HaV3_n0th1ng_But_dr3amS}

这题是原题，脚本参考：

RSA | Lazzaro (lazzzaro.github.io)

eZ_Bl⊕ck

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.strxor import strxor as xor
import os
from secret import flag


def round(s, k):
    l, r = s[:16], s[16:]
    l_, r_ = xor(xor(r, k), l), l
    return l_ + r_


def encode(s, k):
    t = s
    for i in range(8):
        t = round(t, k[i])
    return t


r = os.urandom(32)
print(r)

key = [os.urandom(16) for _ in range(8)]

print(encode(r, key))
m = flag.strip(b'NKCTF{').strip(b'}').replace(b'-', b'')
print(encode(m, key))

# b"t\xf7\xaa\xac\x9d\x88\xa4\x8b\x1f+pA\x84\xacHg'\x07{\xcc\x06\xc4i\xdd)\xda\xc9\xad\xa9\xe8\x1fi"
# b"'{<z}\x91\xda\xc5\xd5S\x8b\xfa\x9f~]J\x0f\xf4\x9a\x1e\xe0\xef\x129N\xe7a\x928+\xe0\xee"
# b'8\x1f"\x83B4\x86)\xce\xebq3\x06\xa0w\x16U\x04M/w\xa1\x8f;)M\xdd~\x11:\xe3\xb3'

题解：

1
2
3
print(encode(r, key))

print(encode(m, key))

这样给了一个例子再给你加密的，要么通过前者求出key，要么两者消掉key，后者居多

八层异或罢了

看不出来就写下来，把每个步骤写下来，不要眼高手低（bushi）

记 r1 = [:16],r2 = [16:],m1 = [:16],m2 = [16:],rc1 = [:16],rc2 = [16:]，mc1 = [:16],mc2 = [16:]

第一层

前一半：r1^r2^key1 后一半：r1

第二层

前一半：r2^key1^key2 后一半：r1^r2^key1

第三层

前一半：r1^key2^key3 后一半：r2^key1^key2

第四层

前一半：r1^r2^key1^key3^key4 后一半：r1^key2^key3

第五层

前一半：r2^key1^key2^key4^key5 后一半：r1^r2^key1^key3^key4

第六层

前一半：r1^key2^key3^key5^key6 后一半：r2^key1^key2^key4^key5

第七层

前一半：r1^r2^key1^key3^key4^key6^key7 后一半：r1^key2^key3^key5^key6

第八层

前一半：r2^key1^key2^key4^key5^key7^key8 后一半：r1^r2^key1^key3^key4^key6^key7

看得出来，m1、m2 同理

第八层

前一半：m2^key1^key2^key4^key5^key7^key8 后一半：m1^m2^key1^key3^key4^key6^key7

所以 m2 = mc1^rc1^r2 ，m1 = mc2^rc2^r1^r2^m2 

1
m = flag.strip(b'NKCTF{').strip(b'}').replace(b'-', b'')

最后拼接转成 uuid 的格式就行了

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import uuid

from Crypto.Util.strxor import strxor as xor

r = b"t\xf7\xaa\xac\x9d\x88\xa4\x8b\x1f+pA\x84\xacHg'\x07{\xcc\x06\xc4i\xdd)\xda\xc9\xad\xa9\xe8\x1fi"
rc = b"'{<z}\x91\xda\xc5\xd5S\x8b\xfa\x9f~]J\x0f\xf4\x9a\x1e\xe0\xef\x129N\xe7a\x928+\xe0\xee"
mc = b'8\x1f"\x83B4\x86)\xce\xebq3\x06\xa0w\x16U\x04M/w\xa1\x8f;)M\xdd~\x11:\xe3\xb3'

r1 = r[:16]
r2 = r[16:]
rc1 = rc[:16]
rc2 = rc[16:]
mc1 = mc[:16]
mc2 = mc[16:]

m2 = xor(xor(mc1,rc1),r2)
m1 = xor(xor(xor(xor(mc2,rc2),r1),r2),m2)
print(uuid.UUID((m1+m2).decode()))

# NKCTF{1ccd5cee-c96d-4caf-8ce5-9a512b3d0655}

easy_high

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from Crypto.Util.number import *
flag = ''

p, q = getPrime(1024), getPrime(1024)
N = p * q
p0 = p ^ (bytes_to_long(flag)<<444)
m = bytes_to_long(flag)
c = pow(m, 65537, N)
print('c=',c)
print('N=',N)
print('p0=',p0)

#c= 4881545863615247924697512170011400857004555681758106351259776881249360423774694437921554056529064037535796844084045263140567168171628832384672612945806728465127954937293787045302307135365408938448006548465000663247116917564500525499976139556325841597810084111303039525833367199565266613007333465332710833102978756654324956219855687611590278570749890543277201538208370370097424105751568285050703167350889953331829275262932104042040526209179357770495596739361176548337593674366015027648541293309465113202672923556991818236011769228078267484362980348613669012975963468592763463397575879215173972436831753615524193609612
#N= 17192509201635459965397076685948071839556595198733884616568925970608227408244870123644193452116734188924766414178232653941867668088060274364830452998991993756231372252367134508712447410029668020439498980619263308413952840568602285764163331028384281840387206878673090608323292785024372223569438874557728414737773416206032540038861064700108597448191546413236875600906013508022023794395360001242071569785940215873854748631691555516626235191098174739613181230094797844414203694879874212340812119576042962565179579136753839946922829803044355134086779223242080575811804564731938746051591474236147749401914216734714709281349
#p0= 149263925308155304734002881595820602641174737629551638146384199378753884153459661375931646716325020758837194837271581361322079811468970876532640273110966545339040194118880506352109559900553776706613338890047890747811129988585025948270181264314668772556874718178868209009192010129918138140332707080927643141811

题解：

我早期的一篇博客写的挺详细的，适合初学者，请移步（划到最后）：RSA刷题系列(施工中) - Wbuildings - 博客园 (cnblogs.com)

把 m 的长度调到 合理范围内就行了

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import libnum, gmpy2

c= 4881545863615247924697512170011400857004555681758106351259776881249360423774694437921554056529064037535796844084045263140567168171628832384672612945806728465127954937293787045302307135365408938448006548465000663247116917564500525499976139556325841597810084111303039525833367199565266613007333465332710833102978756654324956219855687611590278570749890543277201538208370370097424105751568285050703167350889953331829275262932104042040526209179357770495596739361176548337593674366015027648541293309465113202672923556991818236011769228078267484362980348613669012975963468592763463397575879215173972436831753615524193609612
N= 17192509201635459965397076685948071839556595198733884616568925970608227408244870123644193452116734188924766414178232653941867668088060274364830452998991993756231372252367134508712447410029668020439498980619263308413952840568602285764163331028384281840387206878673090608323292785024372223569438874557728414737773416206032540038861064700108597448191546413236875600906013508022023794395360001242071569785940215873854748631691555516626235191098174739613181230094797844414203694879874212340812119576042962565179579136753839946922829803044355134086779223242080575811804564731938746051591474236147749401914216734714709281349
p0= 149263925308155304734002881595820602641174737629551638146384199378753884153459661375931646716325020758837194837271581361322079811468970876532640273110966545339040194118880506352109559900553776706613338890047890747811129988585025948270181264314668772556874718178868209009192010129918138140332707080927643141811
e = 65537

m_length = 400
p_high =(p0>>(m_length+444))<<(m_length+444)

p_low = p0%(2^444)
PR.<x> = PolynomialRing(Zmod(N))
f = p_high+x*2^444+p_low
f = f.monic()
x = f.small_roots(X=2^m_length, beta=0.4)
p = int(p_high+x[0]*2^444+p_low)
q = N//p

d = int(gmpy2.invert(e, (p-1)*(q-1)))
m = int(pow(c, d, N))
print(libnum.n2s(m))

# NKCTF{F10wrs_hVe_r3strDay}

eZ_LargeCG

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
from gmpy2 import next_prime
from Crypto.Util.number import getPrime, isPrime, bytes_to_long
import random
from secret import flag

def init():
    primes = []
    p = 1
    while len(primes) < 100:
        p = next_prime(p)
        primes.append(int(p))
    return primes

def genMyPrimeA(bits):
    while True:
        g = 2
        while g < 2 ** bits:
            g *= random.choice(primes)
        g += 1
        if isPrime(g):
            return g

def genMyPrimeB(bits):
    while True:
        g = 2
        while g < 2 ** bits:
            g *= random.choice(primes)
        g -= 1
        if isPrime(g):
            return g

def gen(st, n, a, b, c, d):
    A = [st + 2023, st + 2024, st + 2025]
    for i in range(6**666):
        A.append((a * A[-3] + b * A[-2] + c * A[-1] + d) % n)
    return A

primes = init()
p1 = getPrime(256)
print(p1)
q1 = 1
while p1 > q1:
    q1 = genMyPrimeA(256)
print(q1)
p2 = getPrime(256)
q2 = 1
while p2 > q2:
    q2 = genMyPrimeB(256)
n1 = p1 * q1
n2 = p2 * q2
print(f'n1 = {n1}')
print(f'n2 = {n2}')

r = getPrime(512)
print(f'r = {r}')

A = gen(bytes_to_long(flag), r, p1, q1, p2, q2)
print(f'A[-3] = {A[-3]}')
print(f'A[-2] = {A[-2]}')
print(f'A[-1] = {A[-1]}')


# n1 = 39755206609675677517559022219519767646524455449142889144073217274247893104711318356648198334858966762944109142752432641040037415587397244438634301062818169
# n2 = 30725253491966558227957591684441310073288683324213439179377278006583428660031769862224980605664642101191616868994066039054762100886678504154619135365646221
# r = 7948275435515074902473978567170931671982245044864706132834233483354166398627204583162848756424199888842910697874390403881343013872330344844971750121043493
# A[-3] = 6085327340671394838391386566774092636784105046872311226269065664501131836034666722102264842236327898770287752026397099940098916322051606027565395747098434
# A[-2] = 1385551782355619987198268805270109182589006873371541520953112424858566073422289235930944613836387546298080386848159955053303343649615385527645536504580787
# A[-1] = 2529291156468264643335767070801583140819639532551726975314270127875306069067016825677707064451364791677536138503947465612206191051563106705150921639560469

题解：

典型的 Pollard’s p-1、William’s p+1 ，脚本参考： RSA | Lazzaro (lazzzaro.github.io)

最后一步是 矩阵快速幂 ，

1
(a * A[-3] + b * A[-2] + c * A[-1] + d) % n

据此构造矩阵

同时 题目说明 p1<q1，p2<q2

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
# python
from gmpy2 import *
from primefac import *

a = 2
k = 2
N = 39755206609675677517559022219519767646524455449142889144073217274247893104711318356648198334858966762944109142752432641040037415587397244438634301062818169

while True:
    a = powmod(a, k, N)
    res = gcd(a-1, N)
    if res != 1 and res != N:
        q = N // res
        print("p1 =",res)
        print("q1 =",q)
        break
    k += 1

n = 30725253491966558227957591684441310073288683324213439179377278006583428660031769862224980605664642101191616868994066039054762100886678504154619135365646221

def mlucas(v, a, n):
    """ Helper function for williams_pp1().  Multiplies along a Lucas sequence modulo n. """
    v1, v2 = v, (v**2 - 2) % n
    for bit in bin(a)[3:]:
        v1, v2 = ((v1**2 - 2) % n, (v1*v2 - v) % n) if bit == "0" else ((v1*v2 - v) % n, (v2**2 - 2) % n)
    return v1

for v in count(1):
    for p in primegen():
        e = ilog(isqrt(n), p)
        if e == 0:
            break
        for _ in range(e):
            v = mlucas(v, p, n)
        g = gcd(v-2, n)
        if 1 < g < n:
            p2 = g
            q2 = n // p2
            print('p2 =',p2)
            print('q2 =',q2)
            exit(0)

        if g == n:
            break

# sage

x = 6085327340671394838391386566774092636784105046872311226269065664501131836034666722102264842236327898770287752026397099940098916322051606027565395747098434    #倒数第三项
y = 1385551782355619987198268805270109182589006873371541520953112424858566073422289235930944613836387546298080386848159955053303343649615385527645536504580787    #倒数第二项
z = 2529291156468264643335767070801583140819639532551726975314270127875306069067016825677707064451364791677536138503947465612206191051563106705150921639560469   #最后一项
r = 7948275435515074902473978567170931671982245044864706132834233483354166398627204583162848756424199888842910697874390403881343013872330344844971750121043493

if p1 > q1:
    p1, q1 = q1, p1
    
if p2 > q2:
    p2, q2 = q2, p2
    
a = p1
b = q1
c = p2
d = q2

mt=matrix(Zmod(r),4,4)
mt[0]=[c,b,a,d]
mt[1]=[1,0,0,0]
mt[2]=[0,1,0,0]
mt[3]=[0,0,0,1]

mn=matrix(Zmod(r),4,1,[z,y,x,1])
X=(mt^(pow(6,666))).solve_right(mn)
print(X)
print(libnum.n2s(int(X[0][0]-2025)))

# NKCTF{y0u_kN0w_r5A_&_LCg_&_Ma7r1X_s0_w3ll!!!}

原题：

RSA中利用光滑数进行模数分解-CSDN博客

complex_matrix

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import *
import gmpy2 as gy
flag = ''


k = 400
p, q = getPrime(741), getPrime(741)
N = p * q
phi = (p-1) * (q-1)
_flag = bytes_to_long(flag)
p, q = getPrime(1024), getPrime(1024)
d_array = [getPrime(k) for _ in range(4)] 
e_array = [inverse(i, phi) for i in d_array]
c = pow(_flag, 65537, N)
print('N:',N)
print('e:',e_array)
print('c:',c)

#N: 71841248095369087024928175623295380241516644434969868335504061065977014103487197287619667598363486210886674500469383623511906399909335989202774281795855975972913438448899231650449810696539722877903606541112937729384851506921675290984316325565141178015123381439392534417225128922398194700511937668809140024838070124095703585627058463137549632965723304713166804084673075651182998654091113119667582720831809458721072371364839503563819080226784026253
#e: [65128799196671634905309494529154568614228788035735808211836905142007976099865571126946706559109393187772126407982007858423859147772762638898854472065889939549916077695303157760259717113616428849798058080633047516455513870697383339784816006154279428812359241282979297285283850338964993773227397528608557211742425548651971558377656644211835094019462699301650412862894391885325969143805924684662849869947172175608502179438901337558870349697233790535, 58756559706647121529575085912021603170286163639572075337348109911506627489265537716060463072086480156516641723700802217411122982693536541892986623158818442274840863016647800896033363360822503445344748132842451806511693779600370832206455202293028402486647422212959763287987847280322100701242139127654031151565924132562837893975505159702015125483479126108892709063135006366792197127007229210558758401679638300464111782814561428899998471531067163715, 34828685390969672139784723764579499920301439564705391196519314224159563070870933754477650614819514127121146216049444888554338415587165719098661141454627820126445291802801256297252654045398330613075575527685542980264993711077876535643646746742646371967302159565887123638001580042027272379341650995728849759541960087953160211696369079708787543303742132161742979856720539914370868829868891655221361545648778590685232034703220732697083024449894197969, 26717968456600556973167180286909817773394160817933525240720067057464671317174201540556176814203780603153696663101158205367554829261808020426363683474848952397963507069306452835776851274959389849223566030857588019845781623271395012194869024566879791449466064832273531795430185178486425688475688634844530106740480643866537205900809400383304665727460014210405339697947582657505028211149470787536144302545259243549176816653560626044921521516818788487]
#c: 39297018404565022956251803918747154798377576057123078716166221329195959669756819453426741569480551313085435037629493881038383709458043802420338889323233368852331387845200216275712388921820794980987541224782392553528127093154957890356084331463340193478391679540506421250562554424770350351514435220782124981277580072039637811543914983033300225131364246910828188727043248991987332274929827173923543187017105236008487756190002204169623313222748976369

题解：

d 为 400bit，N为 741*2 bit，

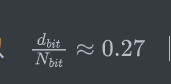
image-20240317145526358

所以，d的大小在Boneh Durfee 攻击范围内

我调的是m=8，求得 d 后就是，已知ed 分解 n

Boneh Durfee 脚本在此 2023年春秋杯网络安全联赛冬季赛 | W’Blog (wbuildings.github.io)

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
e = 65128799196671634905309494529154568614228788035735808211836905142007976099865571126946706559109393187772126407982007858423859147772762638898854472065889939549916077695303157760259717113616428849798058080633047516455513870697383339784816006154279428812359241282979297285283850338964993773227397528608557211742425548651971558377656644211835094019462699301650412862894391885325969143805924684662849869947172175608502179438901337558870349697233790535
d = 2538622943228145345878128391246955913733471093083079525518295718921319603924905551012052344520607070240272805900599777139
n = 71841248095369087024928175623295380241516644434969868335504061065977014103487197287619667598363486210886674500469383623511906399909335989202774281795855975972913438448899231650449810696539722877903606541112937729384851506921675290984316325565141178015123381439392534417225128922398194700511937668809140024838070124095703585627058463137549632965723304713166804084673075651182998654091113119667582720831809458721072371364839503563819080226784026253
c = 39297018404565022956251803918747154798377576057123078716166221329195959669756819453426741569480551313085435037629493881038383709458043802420338889323233368852331387845200216275712388921820794980987541224782392553528127093154957890356084331463340193478391679540506421250562554424770350351514435220782124981277580072039637811543914983033300225131364246910828188727043248991987332274929827173923543187017105236008487756190002204169623313222748976369

import random
import libnum

def factor_with_ed(e,d,n):
    p=1
    q=1
    while p==1 and q==1:
        k = e*d -1
        g = random.randint(1,n)
        while k%2==0:
            k //= 2
            x = pow(g,k,n)
            if x>1 and libnum.gcd(x-1,n)>1:
                p = libnum.gcd(x-1,n)
                q = n//p
    return p,q


p,q = factor_with_ed(e,d,n)
phi = (p-1)*(q-1)
e = 65537
d = libnum.invmod(e,phi)
m = pow(c,d,n)
print(libnum.n2s(int(m)))

# NKCTF{F10w3r_Hav3_r3start_Day_N0_Man_iS_Y0ung_Aga1n}

还可以拓展维纳攻击?

拓展维纳攻击：给了多个指数 $e_i$

Dexterjie师傅测试了3，4，5，6个e，都能够跑出结果，不过跑6个e的需要挺长时间

Xenny给出测试结论：大约8个e 的情况已经运行不出来了

(我才知道这个wiki博客是Xenny师傅的博客，恐怖如斯😭😭)

扩展维纳攻击 - CTF Wiki (ctf-wiki.org)

这边存一下 拓展维纳攻击 的脚本:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
import gmpy2
import libnum
isdigit = lambda x: ord('0') <= ord(x) <= ord('9')

def my_permutations(g, n):
    sub = []
    res = []
    def dfs(s, prev):
        if len(s) == n:
            res.append(s[::])
        for i in g:
            if i in s or i < prev:
                continue
            s.append(i)
            dfs(s, max(prev, i))
            s.remove(i)
    dfs(sub, 0)
    return res

class X3NNY(object):
    def __init__(self, exp1, exp2):
        self.exp1 = exp1
        self.exp2 = exp2
    
    def __mul__(self, b):
        return X3NNY(self.exp1 * b.exp1, self.exp2 * b.exp2)

    def __repr__(self):
        return '%s = %s' % (self.exp1.expand().collect_common_factors(), self.exp2)

class X_Complex(object):
    def __init__(self, exp):
        i = 0
        s = '%s' % exp
        while i < len(s):
            if isdigit(s[i]):
                num = 0
                while i < len(s) and isdigit(s[i]):
                    num = num*10 + int(s[i])
                    i += 1
                if i >= len(s):
                    self.b = num
                elif s[i] == '*':
                    self.a = num
                    i += 2
                elif s[i] == '/':
                    i += 1
                    r = 0
                    while i < len(s) and isdigit(s[i]):
                        r = r*10 + int(s[i])
                        i += 1
                    self.b = num/r
            else:
                i += 1
        if not hasattr(self, 'a'):
            self.a = 1
        if not hasattr(self, 'b'):
            self.b = 0

def WW(e, d, k, g, N, s):
    return X3NNY(e*d*g-k*N, g+k*s)
def GG(e1, e2, d1, d2, k1, k2):
    return X3NNY(e1*d1*k2- e2*d2*k1, k2 - k1)

def W(i):
    e = eval("e%d" % i)
    d = eval("d%d" % i)
    k = eval("k%d" % i)
    return WW(e, d, k, g, N, s)

def G(i, j):
    e1 = eval("e%d" % i)
    d1 = eval("d%d" % i)
    k1 = eval("k%d" % i)
    
    e2 = eval("e%d" % j)
    d2 = eval("d%d" % j)
    k2 = eval("k%d" % j)
    
    return GG(e1, e2, d1, d2, k1, k2)

def R(e, sn): # min u max v
    ret = X3NNY(1, 1)
    n = max(e)
    nn = len(e)
    l = set(i for i in range(1, n+1))
    debug = ''
    u, v = 0, 0
    for i in e:
        if i == 1:
            ret *= W(1)
            debug += 'W(%d)' % i
            nn -= 1
            l.remove(1)
            u += 1
        elif i > min(l) and len(l) >= 2*nn:
            ret *= G(min(l), i)
            nn -= 1
            debug += 'G(%d, %d)' % (min(l), i)
            l.remove(min(l))
            l.remove(i)
            v += 1
        else:
            ret *= W(i)
            l.remove(i)
            debug += 'W(%d)' % i
            nn -= 1
            u += 1
    # print(debug, end = ' ')
    return ret, u/2 + (sn - v) * a

def H(n):
    if n == 0:
        return [0]
    if n == 2:
        return [(), (1,), (2,), (1, 2)]
    ret = []
    for i in range(3, n+1):
        ret.append((i,))
        for j in range(1, i):
            for k in my_permutations(range(1, i), j):
                ret.append(tuple(k + [i]))
    return H(2) + ret
    
def CC(exp, n):
    cols = [0 for i in range(1<<n)]
    
    # split exp
    texps = ('%s' % exp.exp1.expand()).strip().split(' - ')
    ops = []
    exps = []
    for i in range(len(texps)):
        if texps[i].find(' + ') != -1:
            tmp = texps[i].split(' + ')
            ops.append(0)
            exps.append(tmp[0])
            for i in range(1, len(tmp)):
                ops.append(1)
                exps.append(tmp[i])
        else:
            ops.append(0)
            exps.append(texps[i])
    if exps[0][0] == '-':
        for i in range(len(exps)):
            ops[i] = 1-ops[i]
        exps[0] = exps[0][1:]
    else:
        ops[0] = 1
    # find e and N
    l = []
    for i in range(len(exps)):
        tmp = 1 if ops[i] else -1
        en = []
        j = 0
        while j < len(exps[i]):
            if exps[i][j] == 'e':
                num = 0
                j += 1
                while isdigit(exps[i][j]):
                    num = num*10 + int(exps[i][j])
                    j += 1
                tmp *= eval('e%d' % num)
                en.append(num)
            elif exps[i][j] == 'N':
                j += 1
                num = 0
                if exps[i][j] == '^':
                    j += 1
                    while isdigit(exps[i][j]):
                        num = num*10 + int(exps[i][j])
                        j += 1
                if num == 0:
                    num = 1
                tmp *= eval('N**%d' % num)
            else:
                j += 1
        if tmp == 1 or tmp == -1:
            l.append((0, ()))
        else:
            l.append((tmp, tuple(sorted(en))))
    
    # construct h
    mp = H(n)
    for val, en in l:
        cols[mp.index(en)] = val
    # print(cols)
    return cols

def EWA(n, elist, NN, alpha):
    mp = H(n)
    var('a')
    S = [X_Complex(n*a)]
    cols = [[1 if i == 0 else 0 for i in range(2^n)]]
    for i in mp[1:]:
        eL, s = R(i, n)
        cols.append(CC(eL, n))
        S.append(X_Complex(s))
    
    alphaA,alphaB = 0, 0
    for i in S:
        alphaA = max(i.a, alphaA)
        alphaB = max(i.b, alphaB)
    # print(alphaA, alphaB)
    D = []
    for i in range(len(S)):
        # print((alphaA-S[i].a), (alphaB - S[i].b))
        D.append(
            int(NN^((alphaA-S[i].a)*alpha + (alphaB - S[i].b)))
        )
    kw = {'N': NN}
    for i in range(len(elist)):
        kw['e%d' % (i+1)] = elist[i]

    B = Matrix(ZZ, Matrix(cols).T(**kw)) * diagonal_matrix(ZZ, D)
    L = B.LLL(0.5)
    v = Matrix(ZZ, L[0])
    x = v * B**(-1)
    phi = int(x[0,1]/x[0,0]*elist[0])
    return phi

def attack(NN, elist, alpha):
    phi = EWA(len(elist), elist, NN, alpha)
    print(phi)
    return phi


NN = 71841248095369087024928175623295380241516644434969868335504061065977014103487197287619667598363486210886674500469383623511906399909335989202774281795855975972913438448899231650449810696539722877903606541112937729384851506921675290984316325565141178015123381439392534417225128922398194700511937668809140024838070124095703585627058463137549632965723304713166804084673075651182998654091113119667582720831809458721072371364839503563819080226784026253
elist = [65128799196671634905309494529154568614228788035735808211836905142007976099865571126946706559109393187772126407982007858423859147772762638898854472065889939549916077695303157760259717113616428849798058080633047516455513870697383339784816006154279428812359241282979297285283850338964993773227397528608557211742425548651971558377656644211835094019462699301650412862894391885325969143805924684662849869947172175608502179438901337558870349697233790535, 58756559706647121529575085912021603170286163639572075337348109911506627489265537716060463072086480156516641723700802217411122982693536541892986623158818442274840863016647800896033363360822503445344748132842451806511693779600370832206455202293028402486647422212959763287987847280322100701242139127654031151565924132562837893975505159702015125483479126108892709063135006366792197127007229210558758401679638300464111782814561428899998471531067163715, 34828685390969672139784723764579499920301439564705391196519314224159563070870933754477650614819514127121146216049444888554338415587165719098661141454627820126445291802801256297252654045398330613075575527685542980264993711077876535643646746742646371967302159565887123638001580042027272379341650995728849759541960087953160211696369079708787543303742132161742979856720539914370868829868891655221361545648778590685232034703220732697083024449894197969, 26717968456600556973167180286909817773394160817933525240720067057464671317174201540556176814203780603153696663101158205367554829261808020426363683474848952397963507069306452835776851274959389849223566030857588019845781623271395012194869024566879791449466064832273531795430185178486425688475688634844530106740480643866537205900809400383304665727460014210405339697947582657505028211149470787536144302545259243549176816653560626044921521516818788487]
c = 39297018404565022956251803918747154798377576057123078716166221329195959669756819453426741569480551313085435037629493881038383709458043802420338889323233368852331387845200216275712388921820794980987541224782392553528127093154957890356084331463340193478391679540506421250562554424770350351514435220782124981277580072039637811543914983033300225131364246910828188727043248991987332274929827173923543187017105236008487756190002204169623313222748976369
alpha = 400 / int(NN).bit_length()
for i in range(1, len(elist)+1):
    var("e%d" % i)
    var("d%d" % i)
    var("k%d" % i)
g, N, s = var('g'), var('N'), var('s')

for i in range(len(elist)):
    elist[i] = Integer(elist[i])
phi = attack(NN, elist, alpha)

d = gmpy2.invert(65537, phi)
m = int(pow(c, d, NN))
print(libnum.n2s(m))
# NKCTF{F10w3r_Hav3_r3start_Day_N0_Man_iS_Y0ung_Aga1n}

baby_classical（未明白）

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import string
import re
import numpy as np
flag = ''
print('flag length:',len(flag))
dic = string.ascii_uppercase+string.ascii_lowercase+string.digits+'+/'
f1nd = lambda x : dic.find(x)
class KeyEncryption:
    def __init__(self, m: int, fillchar: str="z", key: np.ndarray=None):
        self.m = m
        self.key = key
        self.dicn2s = {i: dic[i] for i in range(64)}
        self.dics2n = dict(zip(self.dicn2s.values(), self.dicn2s.keys()))
        self.fillchar = self.dics2n[fillchar]
    def setM(self, m: int) -> None:
        assert m > 0
        self.m = m
    def setKey(self, key: np.ndarray=None) -> None:
        if key is None:
            while key is None or KeyEncryption.modInv(np.linalg.det(key)) == -1:
                key = np.random.randint(0, 65, size=(self.m, self.m))
            print("random matrix：\n", key)
        else:
            assert KeyEncryption.modInv(np.linalg.det(key)) != -1
        self.key = key
    @staticmethod
    def modInv(x: int):
        y = 0
        while y < 64:
            y += 1
            if (x * y) % 64 == 1:
                return y
        return -1
    def _loopCrypt(self, long: np.ndarray, K: np.ndarray) -> np.ndarray:
        ans = np.array([])
        for i in range(long.shape[0] // self.m):
            ans = np.mod(np.hstack((
                ans, 
                np.dot(long[i*self.m:i*self.m+self.m], K)
            )), 64)
        return ans.astype(np.int64)
    def encrypt(self, plaintext: np.ndarray):
        assert self.m !=None and self.key is not None
        if plaintext.shape[0] % self.m:
            plaintext = np.hstack((
                plaintext, 
                [self.fillchar] *(self.m - plaintext.shape[0] % self.m)
            ))
        return self._loopCrypt(plaintext, self.key)
    def translate(self, s, to: str):
        if to == "text":
            return "".join([self.dicn2s[si] for si in s])
        elif to == "num":
            s = s.replace(" ", "")
            return np.array([self.dics2n[si] for si in s])
def getKey(key):
  he = KeyEncryption(m=3)
  he.setKey()              
  nums = he.translate(key, "num")
  res = he.encrypt(nums)
  enkey = ''.join(dic[i] for i in res.tolist())
  print('Encrypt key:',enkey)
  return enkey
if __name__ == '__main__':
  fir1 = ' '.join(map(lambda _:_[::-1],re.split("[ { _ } ]" , flag.swapcase())))
  ciphertext1 = ''
  key = ""  
  enkey = getKey(key)
  _enkey=[f1nd(i) for i in key]
  print('key lengeh:',len(_enkey))
  j = 0
  for i in fir1:
    if f1nd(i)>=0:
      ciphertext1 += dic[(f1nd(i) + _enkey[j % len(_enkey)])%64]
    else:
      ciphertext1 += i
    j += 1
  ciphertext = ciphertext1.replace(' ','_')
  print('ciphertext:%s{%s}' % (ciphertext[0:5],ciphertext[6:-1]))

'''
flag length: 48
random matrix：
 [[13 37 10]
 [15 17 41]
 [13  0 10]]
Encrypt key: pVvRe/G08rLhfwa
key lengeh: 14
ciphertext:1k2Pe{24seBl4_a6Ot_fp7O1_eHk_Plg3EF_g/JtIonut4/}
'''

题解:

1
2
3
4
5
6
7
8
9
10
11
12
def decrypt(self, ciphertext: np.ndarray) -> str:
    self.key = np.array([[13,37,10],[15,17,41],[13,0,10]])
    print(self.key)
    assert self.m is not None and self.key is not None
    plaintext = ''
    inv_key = KeyEncryption.modInv(np.linalg.det(self.key)) * np.round(
        np.linalg.inv(self.key) * np.linalg.det(self.key))
    for i in range(ciphertext.shape[0] // self.m):
        tmp = np.mod(np.dot(ciphertext[i * self.m:i * self.m + self.m], inv_key), 64)
        plaintext += ''.join([self.dicn2s[int(tmp[j])] for j in range(self.m)])
    plaintext = plaintext.rstrip(self.dicn2s[self.fillchar])
    return plaintext

放弃了，看不懂，存个脚本（我的GPT怎么就写不出来啊）

NKCTF2023·Crypto WP | Harry’s Blog (harry0597.com)

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
import string
import numpy as np

dic = string.ascii_uppercase + string.ascii_lowercase + string.digits + '+/'
f1nd = lambda x: dic.find(x)


class KeyEncryption:
    def __init__(self, m: int, fillchar: str = "z", key: np.ndarray = None):
        self.m = m
        self.key = key
        self.dicn2s = {i: dic[i] for i in range(64)}
        # print("self.dicn2s =", self.dicn2s)
        self.dics2n = dict(zip(self.dicn2s.values(), self.dicn2s.keys()))
        # print("self.dics2n =", self.dics2n)
        self.fillchar = self.dics2n[fillchar]
        # print("fillchar =", self.fillchar)

    def setM(self, m: int) -> None:
        assert m > 0
        self.m = m

    def setKey(self, key: np.ndarray = None) -> None:
        if key is None:
            while key is None or KeyEncryption.modInv(np.linalg.det(key)) == -1:
                key = np.random.randint(0, 65, size=(self.m, self.m))
            # print("random matrix：\n", key)
        else:
            assert KeyEncryption.modInv(np.linalg.det(key)) != -1
        self.key = key

    @staticmethod
    def modInv(x: int):
        y = 0
        while y < 64:
            y += 1
            if (x * y) % 64 == 1:
                return y
        return -1

    def _loopCrypt(self, long: np.ndarray, K: np.ndarray) -> np.ndarray:
        ans = np.array([])
        for i in range(long.shape[0] // self.m):
            ans = np.mod(np.hstack((
                ans,
                np.dot(long[i * self.m:i * self.m + self.m], K)
            )), 64)
        return ans.astype(np.int64)

    def encrypt(self, plaintext: np.ndarray):
        assert self.m != None and self.key is not None
        if plaintext.shape[0] % self.m:
            plaintext = np.hstack((
                plaintext,
                [self.fillchar] * (self.m - plaintext.shape[0] % self.m)
            ))
        # print("plaintext", plaintext)
        return self._loopCrypt(plaintext, self.key)

    def translate(self, s, to: str):
        if to == "text":
            return "".join([self.dicn2s[si] for si in s])
        elif to == "num":
            s = s.replace(" ", "")
            return np.array([self.dics2n[si] for si in s])

    def decrypt(self, ciphertext: np.ndarray) -> str:
        self.key = np.array([[13,37,10],[15,17,41],[13,0,10]])
        print(self.key)
        assert self.m is not None and self.key is not None
        plaintext = ''
        inv_key = KeyEncryption.modInv(np.linalg.det(self.key)) * np.round(
            np.linalg.inv(self.key) * np.linalg.det(self.key))
        for i in range(ciphertext.shape[0] // self.m):
            tmp = np.mod(np.dot(ciphertext[i * self.m:i * self.m + self.m], inv_key), 64)
            plaintext += ''.join([self.dicn2s[int(tmp[j])] for j in range(self.m)])
        plaintext = plaintext.rstrip(self.dicn2s[self.fillchar])
        return plaintext



def getKey(key):
    he = KeyEncryption(m=3)
    he.setKey()
    nums = he.translate(key, "num")
    # print("nums =", nums)

    res = he.encrypt(nums)
    # print('res =', res)
    enkey = ''.join(dic[i] for i in res.tolist())
    # print("res.tolist() =",  res.tolist())
    # print('Encrypt key:', enkey)
    return enkey

he = KeyEncryption(m=3)
enc_key = 'pVvRe/G08rLhfwa'
enc_key = [f1nd(i) for i in enc_key]
# print(enc_key)
enc_key = np.array(enc_key)
# print(enc_key)
key = he.decrypt(enc_key)
# print(key)
_enkey = [f1nd(i) for i in key]

c = '1k2Pe{24seBl4_a6Ot_fp7O1_eHk_Plg3EF_g/JtIonut4/}'
j = 0
tmp = {}
flag = ''
for i in c:
    if f1nd(i) >= 0:
        # tmp = (f1nd(i) + _enkey[j % len(_enkey)]) % 64
        tmp = (f1nd(i) - _enkey[j % len(_enkey)]) % 64
        flag += dic[tmp]
    else:
        flag += i
    j += 1
# print(flag)

for i in flag.split('_'):
    print(i[::-1])
print('CISsALc'[::-1])
#
# 手动转向
flag = 'nkctf{cLAsSIC_C0DE_D0L1S_ArE_R3A1LY_INT3REsTING}'.swapcase()
print(flag)
# NKCTF{ClaSsic_c0de_d0l1s_aRe_r3a1ly_int3reSting}

Raven

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#!/usr/bin/env sage
# Problem by rec, with a bad raven.
import os, hashlib
from Crypto.Util.number import *
from Crypto.Cipher import AES

def Raven(n: int, secret: bytes):
    H = lambda x: hashlib.md5(os.urandom(8) + x).digest()

    p = getPrime(728)
    R.<z> = PolynomialRing(GF(p))

    seed = H(secret)
    f = R(
        [bytes_to_long(secret)] + [bytes_to_long(H(seed)) for _ in range(n - 1)]
    )
    x = [getRandomRange(2, p - 1) for _ in range(n)]
    y = [ZZ(f(xi)^2 + getPrime(256)) for xi in x]

    pairs = list(zip(x, y))
    return p, pairs

flag = b'#####'
key = os.urandom(16)
cipher = AES.new(key=key, IV=bytes(range(16)), mode=AES.MODE_CBC)
ct = cipher.encrypt(flag + os.urandom(16 - len(flag) % 16))
p, pairs = Raven(4, key)

print(f"{p = }\n{pairs = }\n{ct = }")
'''
p = 1018551160851728231474335384388576586031917743463656622083024684199383855595168341728561337234276243780407755294430553694832049089534855113774546001494743212076463713621965520780122783825100696968959866614846174188401153
pairs = [(615358616404864757405587650175842125441380884418119777842292095751090237848084440177153221092040264723889917863863854377665802549748720692225139890884830475485512763149974948701807492663962748292710803434009673589337265, 84982753624462868217739962129526665082932464631118597651920986288766037499319751354013335054886685186857222944776560264528363811382359242656883760986496856164448940929282013856762706210675691655747370624405968909408102), (528363810186974800127873139379943131424126521611531830591311656948009967709310974894584084912262479395720199930206495204352231804549705720854271566421006481173043064265399467682307971910488405265826107365679757755866812, 496810092723839642457928776423789418365006215801711874210443222720529161066621876103037104247173440072986344011599384793861949574577559989016501090247331146721371126871470611440468688947950954988175225633457347666551944), (68711183101845981499596464753252121346970486988311398916877579778110690480447199642602267233989256728822535174215153145632158860662954277116345331672194812126361911061449082917955000137698138358926301360506687271134873, 995428771589393162202488762223106955302099250561593105620410424291405842350539887383005328242236156038373244928147473800972534658018117705291472213770335998508454938607290279268848513727721410314612261163489156360908800), (61574167546312883246262193556029081771904529137922128124933785599227801608271357738142074310192454183183340219301304405636497744152219785042075198056952749425345561162612590170550454476602892138914473795478531165181812, 618169326093802548516842299173393893046765466917311052414967158839652012130855552015876657514610755108820971877570295328618373296493668146691687291894702228119875561585283226588768969944781923428807766632578060221034862)]
ct = b"|2\xf0v7\x05Y\x89\r]\xe93s\rr)#3\xe9\x90%Z\x9a\xd9\x9ck\xba\xec]q\xb8\xf2'\xc8e~fL\xcf\x93\x00\xd6^s-\xc9\xd6M"
'''

题解：

Shamir门限秘密共享方案， SSS，见：

(^▽^)我藏好了哦~Shamir门限方案 | W’Blog (wbuildings.github.io)

1

PsychoRandom

题目

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#!/usr/bin/env python
# Problem by rec, with a toy generator.
import os, utils

seed = int(os.urandom(16).hex(), 16)
gen = utils.ToyGen(seed)

sec = b'#####'
assert b'nkctf' in sec

msg = b'##MSG FROM NK: ' + sec
enc = bytes(m ^ next(gen) for m in msg).hex()
print(enc)
# 9c1250e1fefb6012cf74a7fd0156cd1a2817ee9381d086a1561399f5b7f519e5abf4437739fa254cd35b241375292d73aa8b8e6ff61f4977da3c68a699156e6bfbe2c38d7b08eed07e40e831c25f5327a21847bb156060228e2b

utils.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class ToyGen:
    def __init__(self, state):
        self.nbits = 128
        self.state = state & ((1 << self.nbits) - 1)

        self.mask = 230336355081348639216651218083300669636

        self.alpha = 237299571639771708626086074576623691999
        self.beta = 83015690654496181240783151904447565127

    def func0(self, steps=1):
        for _ in range(steps):
            res = self.state & self.mask
            bit = sum([(res >> i) & 1 for i in range(self.nbits)]) & 1
            self.state = ((self.state << 1) ^ bit) & ((1 << self.nbits) - 1)
        return

    def func1(self):
        res = (self.state ^ self.beta) & self.alpha
        bit = sum([(res >> i) & 1 for i in range(self.nbits)]) & 1
        return bit

    def __next__(self):
        out = 0
        for _ in range(8):
            self.func0(37)
            bit = self.func1()
            out = (out << 1) ^ bit
        return out

题解

Reference：

NKCTF2023·Crypto WP | Harry’s Blog (harry0597.com)

NKCTF | DexterJie’Blog

-------------　　　　本文结束　　感谢阅读　　　　-------------