W'Blog

Wbuildings的自勉小屋

0%

LFSR初探

发表于 分类于 Valine：
本文字数： 5.2k 阅读时长 ≈ 5 分钟

回顾

概述:

线性反馈移位寄存器（LFSR）归属于移位寄存器（FSR）,除此之外还有非线性移位寄存器（NFSR）。移位寄存器是流密码产生密钥流的一个主要组成部分。

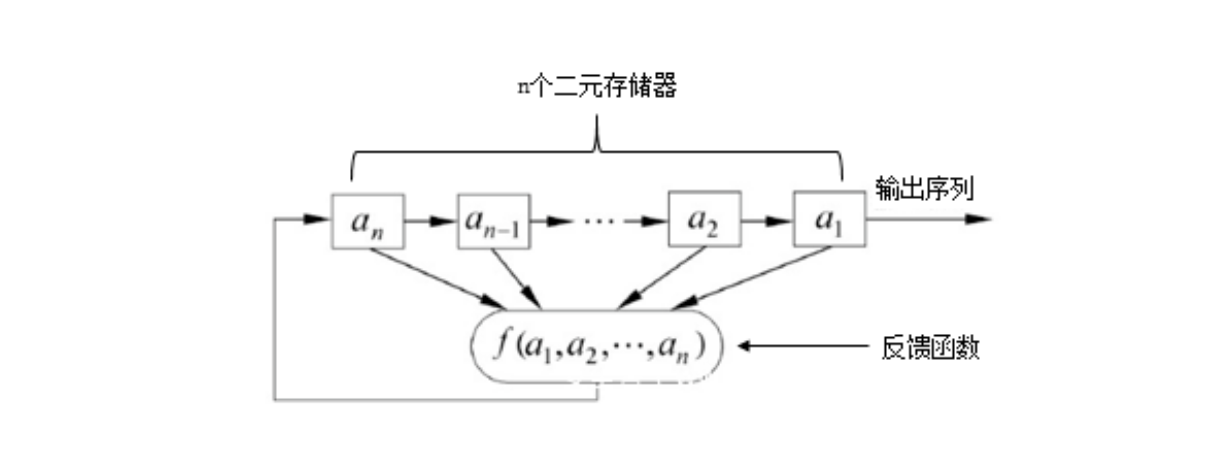
GF(2)上一个n级反馈移位寄存器由n个二元存储器与一个反馈函数
$f(a_1,a_2,…,a_n)$组成，如下图所示。

image-20240809212924563

移位寄存器的三要素：

  • 初始状态：由用户确定
  • 反馈函数：$f(a_1,a_2,…,a_n)$是n元布尔函数，即函数的自变量和因变量只取0和1这两个可能值
  • 输出序列

如果反馈函数是线性的，那么我们称其为 LFSR，此时可以如下表示,：

其中 $c_i={0,1}$

输出序列满足：

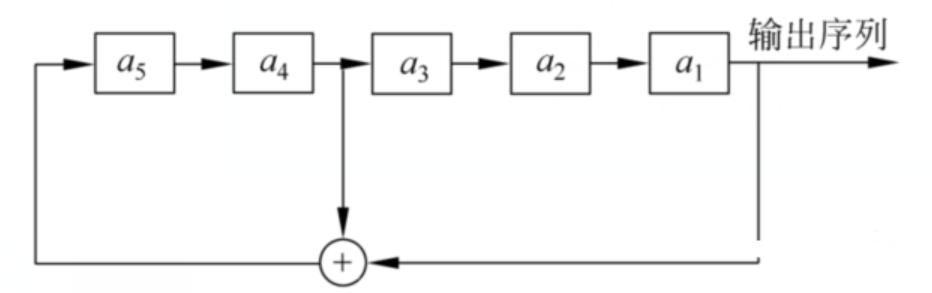
举个栗子：

下面是一个5级的线性反馈移位寄存器，其初始状态为$(a_1,a_2,…,a_n)= (1,0,0,1,1)$

image-20240810100603853

反馈函数为：

(i = 1,2,...)

可以得到输出序列为：

1001101001000010101110110001111 100110…

周期为31。

对于 n 级线性反馈移位寄存器，最长周期为$2^n-1$（排除全零）。达到最长周期的序列一般称为 m 序列

代码辅助理解

1
2
3
4
5
6
7
8
a = '10011'

for i in range(31-len(a)):
    a+= str(int(a[i])^int(a[i+3]))

print(a)

# 1001101001000010101110110001111

栗子：

2018 强网杯 Streamgame1

考点：已知反馈函数，输出序列，求逆推出初始状态

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
# 作用：判断字符串是否以指定字符 开头或结尾
assert len(flag)==25

def lfsr(R,mask):
    output = (R << 1) & 0xffffff #将R向左移动1位，bin(0xffffff)='0b111111111111111111111111'
    i=(R&mask)&0xffffff          #按位与运算符&：参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0
    lastbit=0
    while i!=0:
        lastbit^=(i&1)           #按位异或运算，得到输出序列
        i=i>>1
    output^=lastbit              #将输出值写入 output的后面
    return (output,lastbit)

R=int(flag[5:-1],2)  #flag为二进制数据
mask = 0b1010011000100011100

f=open("key","ab")   #以二进制追加模式打开，如果文件不存在，它将被创建；如果文件已存在，则将在文件末尾追加内容
for i in range(12):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))   #将lfsr输出的序列每8个二进制为一组，转化为字符，共12组
f.close()

攻防世界找到的题，应该是上传者自己的笔记

分析：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def lfsr(R,mask):
    output = (R << 1) & 0xffffff # 将R向左移动1位，bin(0xffffff)='0b111111111111111111111111'
    i=(R&mask)&0xffffff          # 按位与运算符&：参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0
    lastbit=0
    while i!=0:
        lastbit^=(i&1)           # 按位异或运算，得到输出序列
        i=i>>1
    output^=lastbit              # 将输出值写入 output的后面
    return (output,lastbit)

R=int(flag[5:-1],2)  # flag为二进制数据
mask = 0b1010011000100011100
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out

f.write(chr(tmp))

第一次接触的时候就是因为看似复杂的代码逻辑而暂且放弃的，其实也没啥，读！

最后发现这就是三要素中的反馈函数，关注一下 & 运算的意义就行：

（i=1,2,3...）

此题中，c 就是 mask，R就是a，lastbit也就是 $a_{n+i}$ ，并且将out（lastbit）存入key中，

而R和mask的长度都是19位，所以只需取key的前19个数

1
2
3
4
5
6
7
from Crypto.Util.number import *

f = open('key','rb').read()
r = bytes_to_long(f)
print('0'+str(bin(r)[2:20]))

# 0101010100111000111

将 mask 代入进去，只有当 c为 1 的时候 $c_ia_j$ 才可能是 1

$R_{n+i} = (R[-3])⊕(R[-4])⊕(R[-5])⊕(R[-9])⊕(R[-13])⊕(R[-14])⊕(R[-17])⊕(R[-19])$

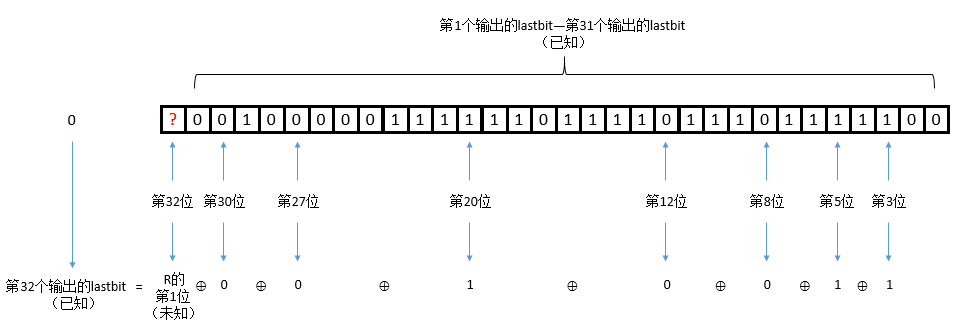
现在我们知道了 key = 0101010100111000111，一位一位异或恢复R即可

key[-1] = 1

$1 = a_{19}⊕(R[-3])⊕(R[-4])⊕(R[-5])⊕(R[-9])⊕(R[-13])⊕(R[-14])⊕(R[-17])$

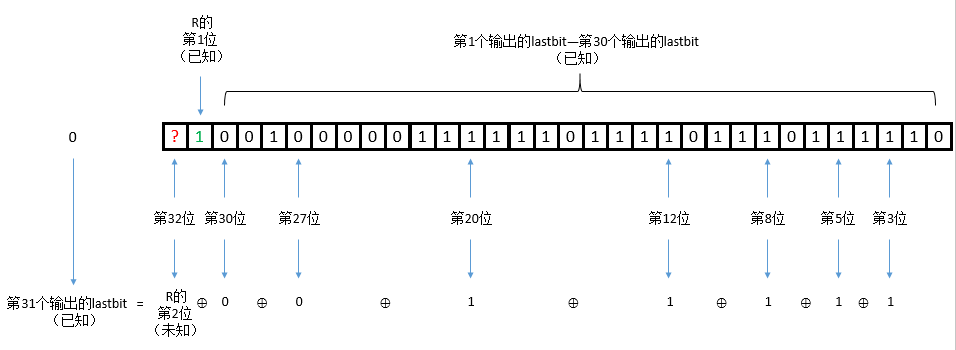
此时 R = key

以此类推 

1
mask = '1010011000100011100'  #顺序 c_n,c_{n-1},。。。,c_1

exp1：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Crypto.Util.number import *

f = open('key','rb').read()
r = bytes_to_long(f)
key = '0'+str(bin(r)[2:20])
# bin_out = bin(r)[2:].zfill(12*8)
# key = bin_out[:19]    

mask = '1010011000100011100'  

R = ''
for i in range(19):
    output = 'x'+key[:18]
    out = int(key[-1])^int(output[-3])^int(output[-4])^int(output[-5])^int(output[-9])^int(output[-13])^int(output[-14])^int(output[-17])
    R += str(out)
    key = str(out)+key[:18]

print('flag{'+R[::-1]+'}')

# flag{1110101100001101011}

exp2：

思路与上面一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
key = '0101010100111000111'
mask = 0b1010011000100011100

R = ""
index = 0
key = key[18] + key[:19]
while index < 19:
    tmp = 0
    for i in range(19):
        if mask >> i & 1:
            tmp ^= int(key[18 - i])
    R += str(tmp)
    index += 1
    key = key[18] + str(tmp) + key[1:18]

print(R[::-1])

exp3:

R，即 seed，构成只有 0，1，爆破系数不大，可以接受

我们可以猜测seed的第19位（0或1），如果seed19+R[:18]输出值等于R[:19]，那么就可以确定seed值了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from Crypto.Util.number import*

f = open('key','rb').read()
c = bytes_to_long(f)
bin_out = bin(c)[2:].zfill(12*8)  

mask = 0b1010011000100011100

def lfsr(R,mask):
    output = (R << 1) & 0xffffffff
    i=(R&mask)&0xffffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)

def blow_up():
    key = bin_out[0:19]      
    tmp = ''
    for i in range(19):
        if lfsr(int('0'+key[0:18],2),mask)[0] == int(key,2):	# 正序
            tmp += '0'
            key = '0'+key[0:18]
        else:
            tmp += '1'
            key = '1' + key[0:18]
    return int(tmp[::-1],2)

r = blow_up()
print(bin(r))

# 1110101100001101011

B-M 算法

如果我们知道了长度为 2n 的输出序列，那么就可以通过构造矩阵来求出 mask,

B-M

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from Crypto.Util.number import *

R = '1000010001101010011111100000110111010011001100011001101100011100000101001000000000000110000011101011100000111010111011101100001001110110001100111010110111011101010111111011011111110010011010010011000011100100010110000011001001011000010111001110010010110001'

X = []
S = []
for i in range(128):
    X.append([int(j) for j in (R[i:i+128])])
    S.append(int(R[128+i]))
    
X = matrix(GF(2), X)
S = vector(GF(2), S)

# print(X.nrows())     # 矩阵行数
# print(X.ncols())	   # 矩阵列数

X = X.inverse()
mask = X * S
# print(mask)

flag = [str(i) for i in mask]
flag = int(''.join(flag),2)
print(b'flag{' + long_to_bytes(flag) + b'}')

Reference：

深入分析CTF中的LFSR类题目（一）-安全客 - 安全资讯平台

CTF竞赛密码学之 LFSR - FreeBuf网络安全行业门户

线性反馈移位寄存器 - LFSR - CTF Wiki (ctf-wiki.org)

彩蛋：

加法 和 异或 的异同

异或

  • 0⊕0=0
  • 0⊕1=1
  • 1⊕0=1
  • 1⊕1=0

加法

  • 0+0=0
  • 0+1=1
  • 1+0=1
  • 1+1=10（在二进制下进位，结果是 0 且产生进位 1）

exp1 理解图

img

9605354f004c487ac512b2e1f2b5e819

-------------　　　　本文结束　　感谢阅读　　　　-------------