再见CBC

又是一道CBC

[安洵杯 2020]easyaes

附件

#!/usr/bin/python
from Crypto.Cipher import AES
import binascii
from Crypto.Util.number import bytes_to_long
from flag import flag
from key import key

iv = flag.strip(b'd0g3{').strip(b'}')

LENGTH = len(key)
assert LENGTH == 16

hint = os.urandom(4) * 8
print(bytes_to_long(hint)^bytes_to_long(key))

msg = b'Welcome to this competition, I hope you can have fun today!!!!!!'

def encrypto(message):
    aes = AES.new(key,AES.MODE_CBC,iv)
    return aes.encrypt(message)

print(binascii.hexlify(encrypto(msg))[-32:])

'''
56631233292325412205528754798133970783633216936302049893130220461139160682777
b'3c976c92aff4095a23e885b195077b66'
'''

还是CBC的题，上面学习了一下填充预言攻击，是已知 IV和 所有密文的一道交互题，这次是一道已知 key和最后一组密文、所有明文的题（key可求，不就是已知的嘛）

据观察，hint 为4字节重复八次而成的一个32字节，而key只有16字节，前后异或求出key

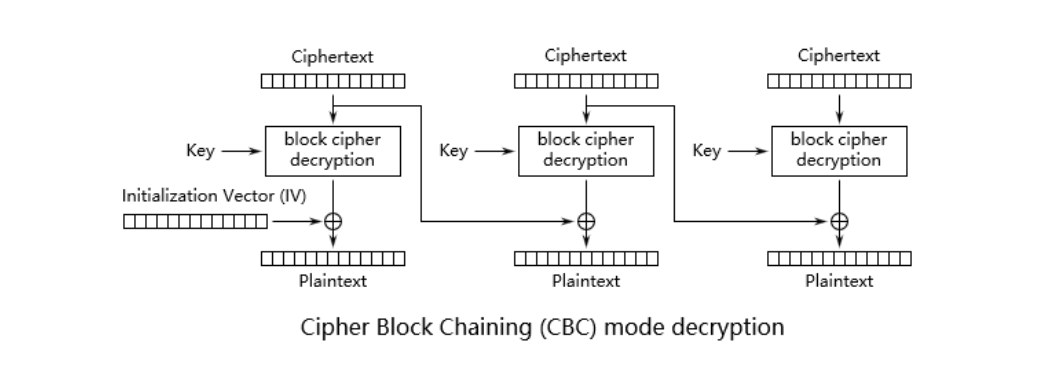
我们再回看一下cbc的解密过程

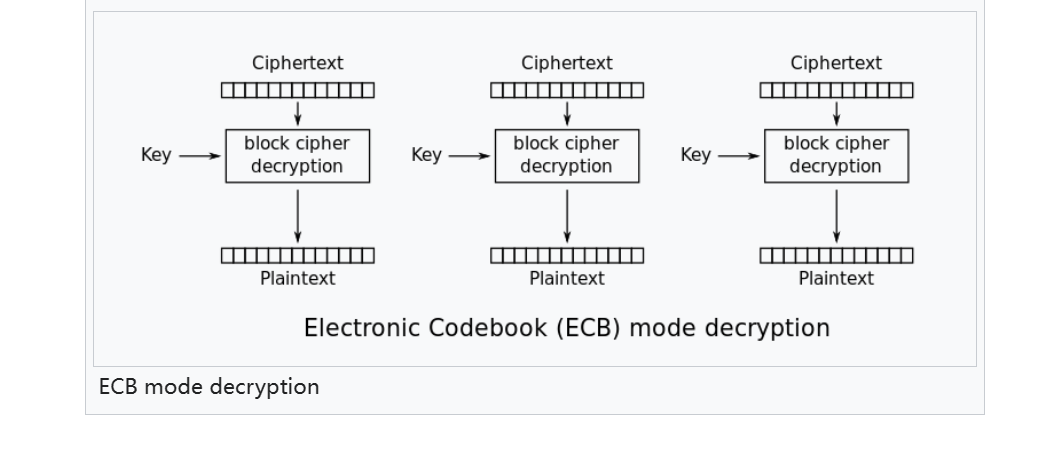
再对比一下 ECB模式的解密过程

前面的步骤是不是惊人的一样，cbc模式就只多了异或 IV

这意味着我们可以通过ECB模式来解CBC模式的前一步骤再和IV异或即可

$定义解密函数dec(enc,key)$

$enc3 = dec(enc4,key)\oplus msg[3]$

$enc2 = dec(enc3,key)\oplus msg[2]$

$enc1 = dec(enc2,key)\oplus msg[1]$

$IV = dec(enc1,key)\oplus msg[0]$

得解

exp：

from Crypto.Util.number import *
from Crypto.Cipher import AES
from Crypto.Util.strxor import strxor

xor = 56631233292325412205528754798133970783633216936302049893130220461139160682777
xor = long_to_bytes(xor)
key = long_to_bytes(bytes_to_long(xor[:16]) ^ bytes_to_long(xor[16:]))

msg = b'Welcome to this competition, I hope you can have fun today!!!!!!'
msgs = [msg[i:i+16] for i in range(0,len(msg),16)]
print(msgs)

enc4 = '3c976c92aff4095a23e885b195077b66'
IV = bytes.fromhex(enc4)

def dec(m,key,enc):
    aes = AES.new(key,AES.MODE_ECB)
    enc = strxor(aes.decrypt(enc),m)
    return enc

for m in msgs[::-1]:
    IV = dec(m,key,IV)

print(b'd0g3{' + IV+ b'}')

# d0g3{aEs_1s_SO0o_e4sY}